Memorization Dynamics in Knowledge Distillation for Language Models

Knowledge Distillation (KD) is increasingly adopted to transfer capabilities from large language models to smaller ones, offering significant improvements in efficiency and utility while often surpassing standard fine-tuning. Beyond performance, KD is also explored as a privacy-preserving mechanism to mitigate the risk of training data leakage. While training data memorization has been extensively studied in standard pre-training and fine-tuning settings, its dynamics in a knowledge distillation setup remain poorly understood. In this work, we study memorization across the KD pipeline using three large language model (LLM) families (Pythia, OLMo-2, Qwen-3) and three datasets (FineWeb, Wikitext, Nemotron-CC-v2). We find: (1) distilled models memorize significantly less training data than standard fine-tuning (reducing memorization by more than 50%); (2) some examples are inherently easier to memorize and account for a large fraction of memorization during distillation (over ~95%); (3) student memorization is predictable prior to distillation using features based on zlib entropy, KL divergence, and perplexity; and (4) while soft and hard distillation have similar overall memorization rates, hard distillation poses a greater risk: it inherits $2.7\times$ more teacher-specific examples than soft distillation. Overall, we demonstrate that distillation can provide both improved generalization and reduced memorization risks compared to standard fine-tuning.

The Llama 4 Herd: Architecture, Training, Evaluation, and Deployment Notes

This document consolidates publicly reported technical details about Metas Llama 4 model family. It summarizes (i) released variants (Scout and Maverick) and the broader herd context including the previewed Behemoth teacher model, (ii) architectural characteristics beyond a high-level MoE description covering routed/shared-expert structure, early-fusion multimodality, and long-context design elements reported for Scout (iRoPE and length generalization strategies), (iii) training disclosures spanning pre-training, mid-training for long-context extension, and post-training methodology (lightweight SFT, online RL, and lightweight DPO) as described in release materials, (iv) developer-reported benchmark results for both base and instruction-tuned checkpoints, and (v) practical deployment constraints observed across major serving environments, including provider-specific context limits and quantization packaging. The manuscript also summarizes licensing obligations relevant to redistribution and derivative naming, and reviews publicly described safeguards and evaluation practices. The goal is to provide a compact technical reference for researchers and practitioners who need precise, source-backed facts about Llama 4.

Resampling methods for Private Statistical Inference

We consider the task of constructing confidence intervals with differential privacy. We propose two private variants of the non-parametric bootstrap, which privately compute the median of the results of multiple ``little'' bootstraps run on partitions of the data and give asymptotic bounds on the coverage error of the resulting confidence intervals. For a fixed differential privacy parameter $\epsilon$, our methods enjoy the same error rates as that of the non-private bootstrap to within logarithmic factors in the sample size $n$. We empirically validate the performance of our methods for mean estimation, median estimation, and logistic regression with both real and synthetic data. Our methods achieve similar coverage accuracy to existing methods (and non-private baselines) while providing notably shorter ($\gtrsim 10$ times) confidence intervals than previous approaches.

Differentially Private Heavy Hitter Detection using Federated Analytics

In this work, we study practical heuristics to improve the performance of prefix-tree based algorithms for differentially private heavy hitter detection. Our model assumes each user has multiple data points and the goal is to learn as many of the most frequent data points as possible across all users' data with aggregate and local differential privacy. We propose an adaptive hyperparameter tuning algorithm that improves the performance of the algorithm while satisfying computational, communication and privacy constraints. We explore the impact of different data-selection schemes as well as the impact of introducing deny lists during multiple runs of the algorithm. We test these improvements using extensive experimentation on the Reddit dataset~\cite{caldas2018leaf} on the task of learning the most frequent words.

Private optimization in the interpolation regime: faster rates and hardness results

In non-private stochastic convex optimization, stochastic gradient methods converge much faster on interpolation problems -- problems where there exists a solution that simultaneously minimizes all of the sample losses -- than on non-interpolating ones; we show that generally similar improvements are impossible in the private setting. However, when the functions exhibit quadratic growth around the optimum, we show (near) exponential improvements in the private sample complexity. In particular, we propose an adaptive algorithm that improves the sample complexity to achieve expected error $\alpha$ from $\frac{d}{\varepsilon \sqrt{\alpha}}$ to $\frac{1}{\alpha^\rho} + \frac{d}{\varepsilon} \log\left(\frac{1}{\alpha}\right)$ for any fixed $\rho >0$, while retaining the standard minimax-optimal sample complexity for non-interpolation problems. We prove a lower bound that shows the dimension-dependent term is tight. Furthermore, we provide a superefficiency result which demonstrates the necessity of the polynomial term for adaptive algorithms: any algorithm that has a polylogarithmic sample complexity for interpolation problems cannot achieve the minimax-optimal rates for the family of non-interpolation problems.

Fine-tuning is Fine in Federated Learning

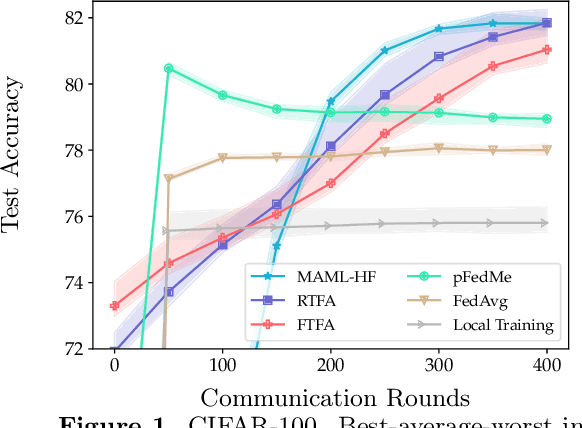
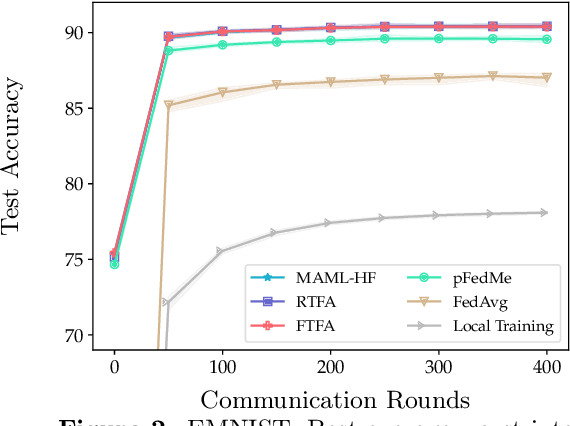
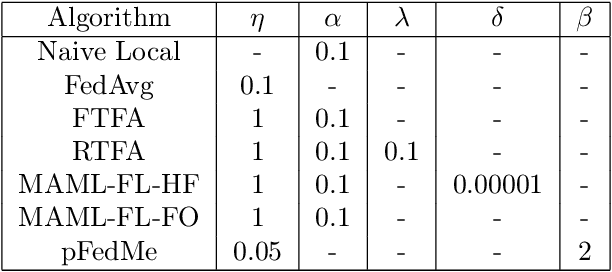
We study the performance of federated learning algorithms and their variants in an asymptotic framework. Our starting point is the formulation of federated learning as a multi-criterion objective, where the goal is to minimize each client's loss using information from all of the clients. We propose a linear regression model, where, for a given client, we theoretically compare the performance of various algorithms in the high-dimensional asymptotic limit. This asymptotic multi-criterion approach naturally models the high-dimensional, many-device nature of federated learning and suggests that personalization is central to federated learning. Our theory suggests that Fine-tuned Federated Averaging (FTFA), i.e., Federated Averaging followed by local training, and the ridge regularized variant Ridge-tuned Federated Averaging (RTFA) are competitive with more sophisticated meta-learning and proximal-regularized approaches. In addition to being conceptually simpler, FTFA and RTFA are computationally more efficient than its competitors. We corroborate our theoretical claims with extensive experiments on federated versions of the EMNIST, CIFAR-100, Shakespeare, and Stack Overflow datasets.

Accelerated, Optimal, and Parallel: Some Results on Model-Based Stochastic Optimization

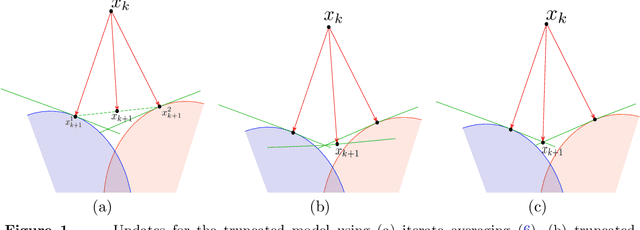
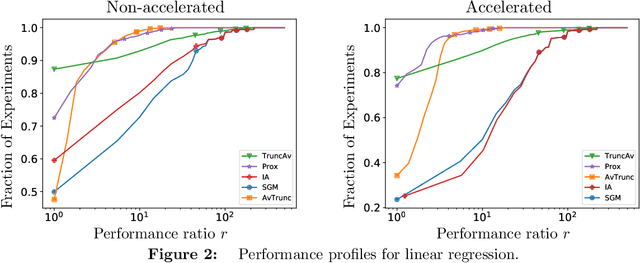
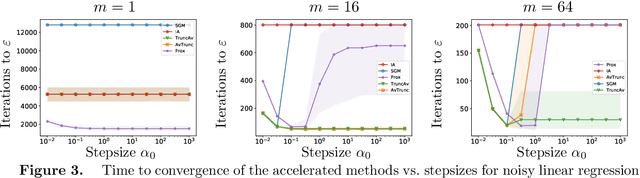
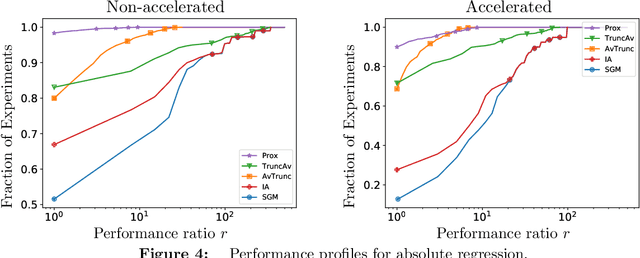
We extend the Approximate-Proximal Point (aProx) family of model-based methods for solving stochastic convex optimization problems, including stochastic subgradient, proximal point, and bundle methods, to the minibatch and accelerated setting. To do so, we propose specific model-based algorithms and an acceleration scheme for which we provide non-asymptotic convergence guarantees, which are order-optimal in all problem-dependent constants and provide linear speedup in minibatch size, while maintaining the desirable robustness traits (e.g. to stepsize) of the aProx family. Additionally, we show improved convergence rates and matching lower bounds identifying new fundamental constants for "interpolation" problems, whose importance in statistical machine learning is growing; this, for example, gives a parallelization strategy for alternating projections. We corroborate our theoretical results with empirical testing to demonstrate the gains accurate modeling, acceleration, and minibatching provide.